14. mars er ingen vanlig Pi-dag i år. Matte-entusiaster overalt feirer arrangementet som Ultimate Pi Day, fordi datoen vil tilsvare de fem første sifrene i pi (3.1415) i stedet for bare de tre første. Denne matematiske samløpet kommer ikke igjen på et århundre, 14. mars 2115.
Relatert innhold
- Verden er full av sirkler
Definert som forholdet mellom en sirkels omkrets og dens diameter, er pi ( π ) både et transcendentalt og et irrasjonelt tall, noe som betyr at den aldri kan skrives som forholdet mellom to hele tall, og det fortsetter på ubestemt tid uten noe gjentagende mønster. Pi er ikke det eneste irrasjonelle tallet - det er også Eulers antall (e) og det gyldne forholdet ( φ eller phi), for eksempel. Men det fortsetter å være en kilde til fascinasjon fordi opprinnelsen er lett forklarbar, sier Mario Livio, en astrofysiker ved Space Telescope Science Institute i Maryland.
”Alle kan forstå hvordan pi er avledet. Alle de andre tallene er mer sammensatte. Tallet phi innebærer for eksempel en bestemt inndeling av en linje, og tallet e krever at du vet hva en logaritme er, sier Livio, forfatter av boken Er Gud en matematiker?
En annen stor del av pis appell er at den har en uhyggelig evne til å vises i matematiske formler, hvorav mange er viktige for daglige prosesser, fra bildebehandling til GPS-navigasjon. Her er bare en liten prøvetaking av de ofte brukte formlene som inkluderer pi:
Fourier-transformasjonen
Oppkalt etter den franske matematikeren Jean-Baptiste Joseph Fourier, dekomponerer dette matematiske verktøyet et signal i komponentfrekvensene - snarere som hvordan en musikalsk akkord kan deles inn i komponentnotene. I hovedsak er Fourier-transformasjoner ideelle for å behandle bølgebaserte signaler som lyd eller lys og for å finne mønstre. Det gjør Fourier-transformasjonen til et grunnleggende verktøy i den moderne digitale verdenen.
“Det har blitt kalt den viktigste algoritmen som noen gang er utviklet av menneskeheten. Nå kan det være hyperbole, men kanskje er det ikke det, sier Glen Whitney, grunnlegger og direktør for National Museum of Mathematics i New York City. Fourier-transformasjoner brukes hele tiden for å rydde opp i digitale bilder, til Auto-Tune popstjerner og for å finne fjerne planeter som kretser rundt andre stjerner. Verktøyet er også avgjørende for tale-til-tekst-funksjonene som nå er standard på smarttelefoner. "Når du bruker Siri eller Google Nå, er et av de første trinnene å ta stemmen din og gjøre en Fourier-transformasjon på den ... det viser seg å være mye lettere å gjenkjenne vokaler når du ser på Fourier-transformasjonene enn når du ser på originale signaler selv, sier Whitney.
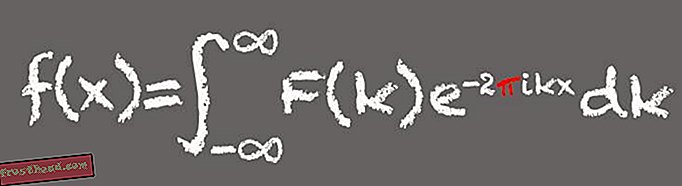(Illustrasjon av Victoria Jaggard) Pi vises i Fourier-transformasjonen fordi en av komponentdelene, eller uttrykkene, av formelen er assosiert med sinus og kosinus og vinklene skapt av en partikkel som beveger seg rundt en sirkel. "Når du har en formel som omhandler sirkler eller vinkler, kommer du ikke til å bli overrasket når pi dukker opp, " sier Whitney.
Heisenberg usikkerhetsprinsipp
En av bærebjelkene i kvantemekanikk, Heisenbergs usikkerhetsprinsipp sier at en observatør ikke kan vite både plasseringen og hastigheten til en subatomisk partikkel samtidig. I stedet, jo mer presist en partikkels posisjon er kjent, desto mindre kan man vite om dens hastighet.
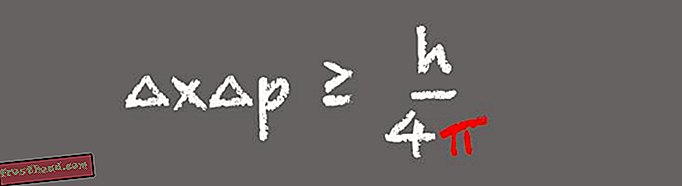(Illustrasjon av Victoria Jaggard) Utseendet til pi i Heisenbergs usikkerhetsprinsipp er fornuftig når du innser at i formelen, posisjonen og momentumet er Fourier transformasjoner av hverandre, sier Whitney. Usikkerhetsprinsippet er viktig i den moderne verden fordi det beskriver oppførselen til lyspartikler, eller fotoner, i fiberoptiske kommunikasjonssystemer. "Det det forteller oss, er at vi ikke kan vite både fotonens posisjon og fremdrift med ekstrem presisjon. Du kan ikke utforme kommunikasjonsprotokoller som bryter Heisenbergs usikkerhetsprinsipp, fordi de ikke vil fungere. ”
Stoke's Law
Stokes lov beregner kraften som trengs for å bevege en liten sfære - det vil si en tredimensjonal sirkel - gjennom en tyktflytende væske med en viss hastighet. Den har applikasjoner innen felt som spenner fra jordvitenskap til medisin.
(Illustrasjon av Victoria Jaggard) "Loven handler spesifikt om effekten av viskositet på en sfære i væsken, " sier Whitney, og det er slik pi kommer inn i bildet. Når det gjelder praktisk bruk av Stokes lov, må du ikke se lenger enn bilen din. "I flere tiår var måten selskapene sørget for at motoroljen din hadde riktig viskositet for bilen din på å bokstavelig talt slippe en serie testsfærer i oljen og måle tiden det tar dem å falle gjennom væsken, " sier Whitney. I dag involverer den vanligste måten å måle oljeviskositet på et verktøy som kalles et kapillærrørviskometer, ingen sfærer er nødvendig - men det rapporterer fortsatt om resultatet i måleenheter som kalles centistoke.
Eulers formel
Oppkalt etter den sveitsiske matematikeren Leonard Euler, samler versjonen av denne formelen som inkluderer pi noen av de mest spennende tallene i matematikk på ett sted:
(Illustrasjon av Victoria Jaggard) “Alle synes bare dette er utrolig. Alle disse tallene som vi anser som spesielle vises i en vakker ligning, sier Livio. Selv om denne småformelen kan inspirere ærefrykt hos matematikere, er den mer nyttige formen for ligningen litt lenger:
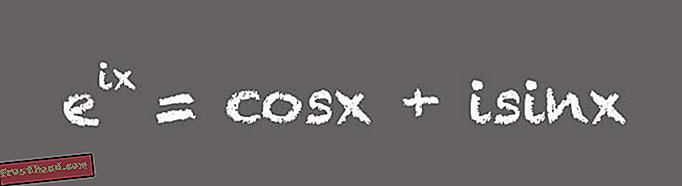(Illustrasjon av Victoria Jaggard) Denne utpakket versjonen av Euler formel er et utrolig verktøy, sier Whitney. For eksempel er det viktig for å designe elektronikk som bruker vekselstrøm, eller vekselstrøm. "Eulers formel i den utvidede formen betyr at du kan bruke komplekse eller imaginære tall for å analysere og designe vekselstrømskretser, " sier Whitney. Det skyldes at i en vekselstrømskrets er spenningen en mengde som svinger over tid - vanligvis 60 ganger per sekund, for eksempel i standard amerikansk elektrisk forsyning. "Den fulle versjonen av Eulers formel lærer hvordan vi kan bruke komplekse tall som et praktisk stykke kort for å modellere svingende fenomener, " sier Whitney.
Einsteins feltlikninger
Albert Einsteins feltlikninger beskriver hvordan tyngdekraften fra masse og energi skaper romtidens krumning som en kjernekomponent i hans generelle relativitetsteori.
(Illustrasjon av Victoria Jaggard) "Å beskrive at krumning innebærer geometri, og siden den opprinnelige definisjonen av pi kommer fra geometri, er det ikke så overraskende at utseendet i denne ligningen, " sier Livio. I tillegg til å avsløre en grunnleggende sannhet om hvordan universet fungerer, har generell relativitet mange praktiske anvendelser. For eksempel ville satellittene som utgjør det globale posisjoneringssystemet som brukes til navigasjon, håpløst være synkronisert med hverandre hvis ingeniørene ikke tok hensyn til tidsutvidelseseffektene som er forutsagt av teorien.
